2021年3月17日下午，张露老师执教了五下的《探索图形面积中的变化规律》这一课。听完这节课，我感受颇深，张老师这节课最主要有以下两方面的特点：

一、知识脉络清晰，教师从扶到放，让学生逐步完成规律的探索。

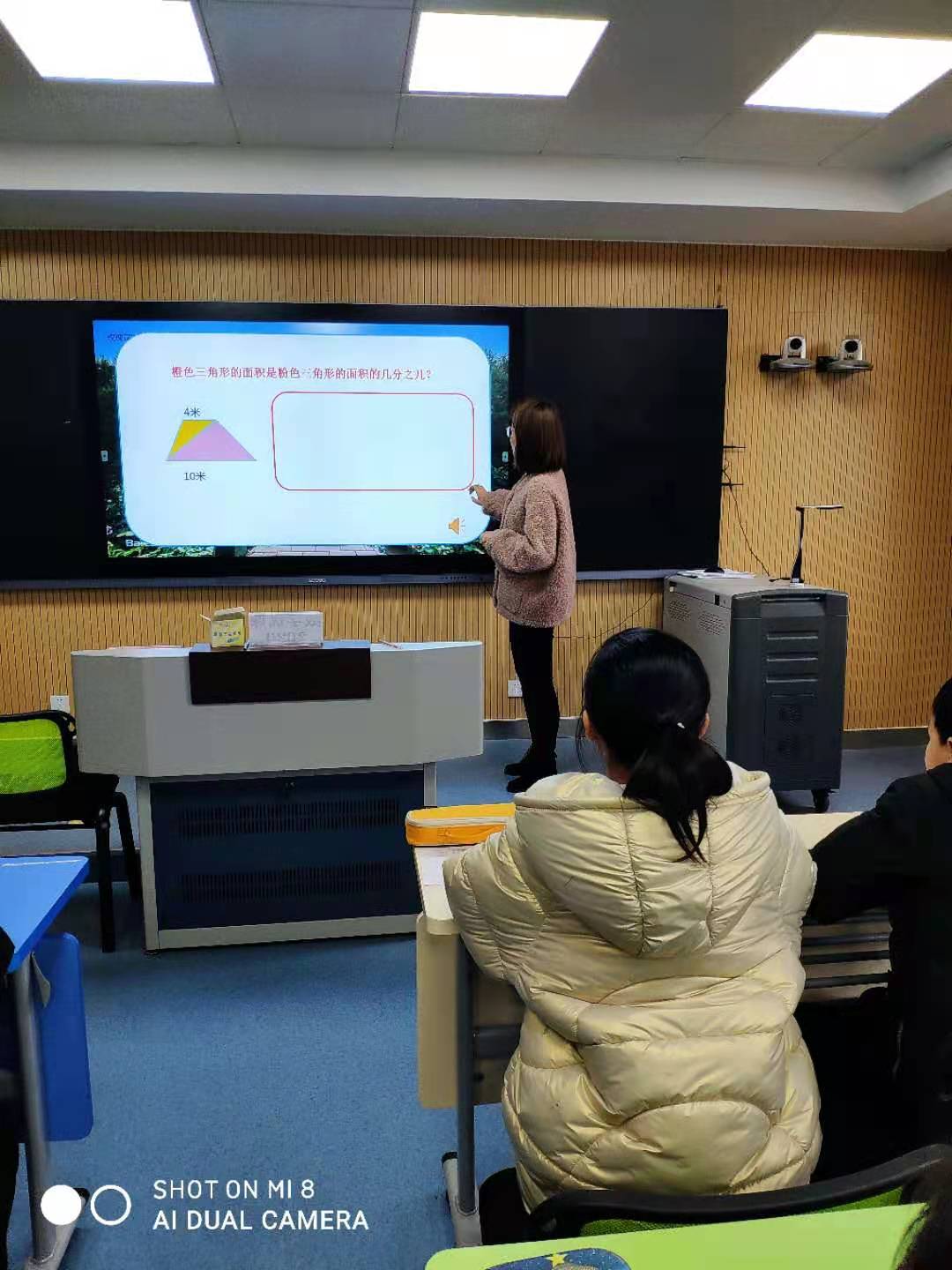
刚开始，张老师出示了两个三角形，分别已知高和底的长度求出它们的面积。这一步旨在让学生回忆求三角形面积的公式和方法，为下面的探索学习作了知识铺垫；接下来又出示了两个三角形等高情况下的两个问题：（1）橙色三角形面积是粉色三角形面积的几分之几；（2）梯形面积是粉色三角形面积的几分之几。在解决前一个问题时，张老师注重引导学生思考：高的条件不知道，可不可以进行假设？学生各抒己见，假设的数据各不相同。在让学生根据自己的设定列式解决问题之后，引导学生进行比较，发现不管假设的数据是几，最后的结果都是一样的，学生陷入了思考。接着老师又抛出了后一个问题，这一次老师不作任何提示，让学生根据自己在上一题中获得的经验独自解决这道题。学生的表现让人惊喜，有的学生假设高为具体的数据，也有学生想到用字母h代替，后一种学生的思维层次明显得到了提升。

在此基础上，张老师又出示了两个等底三角形的问题：绿色三角形面积是红色三角形面积的几分之几。这个问题，学生的答案比较有意思，一个学生假设底为1，更多的学生是假设底为a，计算过程都比较简洁。看来，大多数学生已经能探索出这些图形面积的内在规律了，即不管是等高还是等底的两个三角形，在不知道高或是底条件的情况下，不管是用数字来代替还是用字母代替，两个三角形面积的比都是固定的。

三次问题的依次呈现，使得学生的思考逐步走向深入，从假设数据的多元化逐步趋向单一的用字母表示，学生的思维经历了假设、比较、类比、概括、归纳这一系列的活动过程，使得学生的思维品质不断得到提升和发展。

二、问题的递进呈现，使得数学深度学习真实发生。

在学生经历一番思维探索初次品尝到成功的喜悦之后，张老师又抛出了最后一个问题：小小设计师，让学生根据今天学习的内容把一个三角形分成两个三角形，使一个三角形的面积是另一个三角形面积的1/4。

学习数学的最终目的是数学的应用。规律的探索学习过程一般是学生经过探索之后发现规律，再到运用规律解决问题。数学源于生活用于生活，这个问题很具有挑战性，要求学生将刚刚获得的知识灵活地进行运用。学生在经过片刻的思考之后，在张老师的循循善诱之下，想到了将三角形的底分成5等份，让后将它分为1和4，这样一个三角形面积就是另一个三角形面积的1/4。这个问题是规律的具体应用，在探究规律的过程中，教师不断启发、引导学生思考，以问题驱动学生学习，培养了学生的问题解决能力，学生获得的成就感为他们持续学习提供了动力。由于时间关系，张老师无法留给学生足够的时间来交流和展示，答案肯定不止一种，我想课后肯定会有学生继续思考：还没有别的设计方案。这样的学习过程使得学生的思维更深刻，学习变得更有意义，从而使学生的深度学习真实发生。